Recommend AIRS 모델링 & 시스템
18 Jul 2020 ML: 자세한 추천 시스템 공부에 앞서, 네이버 뉴스 추천 시스템인 AIRS개발과정을 토대로, 추천시스템의 주요 골자와 현황, 예상되는 문제점등을 살펴보자.
1. 추천 모델링이란?
1-1) 추천 모델링 정의
: 특정 ‘시점’에 유저가 ‘좋아할’ 만한 아이템의 리스트를 찾는 것
- 추천 모델링 [유저(나이 / 성별)정보 + 로그(관람 이력) 데이터 + 아이템(영화) 정보]
특정 영화할 좋아할 만한 사람 & 그 사람이 영화를 보고 싶은 시점
1-2) 추천 모델링 고려사항
- 유저수(관객수)
-
- 아이템 수
- 추천해야 하는 아이템(영화)의 수
(1) 과거 영화 → 학습의 목표
(2) 신규 영화 → 최종 목표
-
- 업데이트 양 / 주기
- 새로운 아이템(영화)이 출시되는 양과 주기
- 모델 복잡도
-
- 시스템 성능
- 모델 복잡도와 시스템 성능간의 trade-off관계(우도할거)
1-3) 추천 모델링 난제
-
- Sparsity Problem
- 유저와 아이템 개수가 급증할 수록,
유저가 실제 소비한 아이템의 비율은 점점 줄어듦
→ 추천 피드백 정보가 희박해짐
→ 영화 데이터의 경우, 유저가 실제 소비한 아이템이 더욱 적어 현재 Sparsitiy Problem이 가장 크게 우려됨.
1-4) 추천 모델링 프로세스
- log 분석
- 모델 선정
- 모델 학습
- 품질 평가
- A|B 테스트
- 서비스 적용
→ 위 단계가 Loop를 돌며 반복됨
2. 추천 모델의 종류
Q. 유저가 좋아할 만한 아이템의 정의가 뭐지?
A. 추천 모델마다 정의가 달라진다.
- Statistics Based
- Collaborative Filtering
- Deep Learning
→ 이는 추천 알고리즘이라고 해서, 무조건 협업필터링이 좋은 것이 아니라, 적용하려는 서비스에 가장 잘 어울리는 ‘좋아할 만한’의 의미 그리고, 시스템 부하값 등을 고려해서 모델을 선택하는 과정이 우선적으로 필요.
2-1) Statistics Based
“좋아할 만한 = 통계적으로 유의미한 아이템”
- Chi-squared (category)
$ : X^2 = sum{(x_i - m_i)^2/m_i}$- 원래 모집단과 표본이 있을 때, 모집단과 표본이 얼만큼 다른가를 검증하는 방법.
- 유저가 소비한 아이템의 예측치(m_i)와 실제로 소비한 관측치(x_i)의 차이를 이용
- 절대적인 값보다는 상대적인 변화량에 주목해 하나의 새로운 feature로 활용
- Cross-Entropy & KL-divergence (Continuous Variable)
$: H(p,q) = - \sum_{k=1}^N p(x)log q(x)$- p(x) : 관측치 , q(x) : 예측치
- KLD : 두개의 분포(p&q)가 있을 때, p분포가 q분포로 얼만큼 설명될 수 있는가(=분포의 차이가 얼만큼 큰가).
→ 정보 손실량을 측정하기 위한 방법
ML) 관측 엔트로피 = 학습(train set)의 엔트로피 —> 모델 구축시 모델의 하이퍼 파라미터를 결정할 때, 관측 데이터의 엔트로피는 필요없음(모델이 얼마나 더 좋은지를 알기 위해서는 예측분포와 관측분포간 차이만 알면 되기에 그래서 보통 관측엔트로피를 뺀부분만 loss function으로 사용하게 됨.
RC) 그러나 추천 모델에선 예측 분포와 관측 분포간 얼마나 차이가 나는가에 따라, 차이가 난다는 것은 의외성이 있는 추천을 해줄 수 도 있음을 의미함
2-2) Collaborative Filtering
“좋아할 만한 = 나와 비슷한 유저가 좋아한 아이템”
(1) Neighborhood models
: 유저-유저 / 아이템-아이템 간의 similarity(유사도) 계산
- User-based : 함께 본 문서 수
-
- Item-based : 함께 본 유저 수
- but User-based & Item-based 둘다 유사도 계산 과정에서 반대편 정보를 압축하는 과정이 발생하기에 정보 손실이 발생
- 유사도 측정 방법
- Cosi ne Similarity
: 벡터의 내적 - Jaccard Index
: 교집합 - PMI(pointwise Mutual Information)
: 함께 발생한 빈도와 함께 각 이벤트가 발생할 확률을 함께 고려한 정보량(빈도만 고려하는 앞서 두 방법보다, 확률을 고려하기에 더 좋은 성능)
- Cosi ne Similarity
(2) Matrix Factorization Models
: 유저와 아이템간의 상호작용 데이터를 기반으로 은닉인자를 찾아냄 → item-vector와 user-vector간 내적으로 계산
-
Prediction
$ \hat{r}_{ui} = x_u^T \cdot y_i $
-
Loss function
$L = \sum(r_{ui} - x_u^T \cdot y_i)^2 +( \lambda_x\sum_u ||x_u||^2 +\lambda_x\sum_u ||y_i||^2) $
오차 = (관측치 - 예측치) + (L2 regularization) - Limitations
- 계산량이 많고 학습 속도가 느림
- missing data를 negative 샘플로 사용하기에
-
- wALS
- 계산량 및 학습 속도 문제 해결을 위해 한쪽의 파라미터를 고정하고 반대편 파라미터를 추정하는 방법 → 이때도, 위에서 언급한 missing data를 어떻게 튜닝할 것인가에 따라 성능이 달라진다. —
2-3) Deep Learning
“좋아할 만한 = 나와 컨텍스트 벡터 와 가까운 아이템을 찾는 것” : 유저와 아이템이 벡터로 표현될 수 있을 때, 인공신경망을 통해 유저-아이템 관계 추론
- +Non Linear Models..!!
(1) RNN
: 유저의 문서 소비 패턴을 보고 추천
- 신규 뉴스의 경우 유저 로그가 없는 상태임
- RNN을 통해 학습된 유저 임베딩 정보를 활용
- 유저-문서간 벡터연산을 통해 뉴스를 추천
(→ 신규 영화 개봉작 역시 유저로그가 없음)

(2) CNN
: 문서내 단어들의 배열을 보고 주제를 추론
(3) Deep CF Models
: Deep Learning과 CF를 함께 고려하는 방법
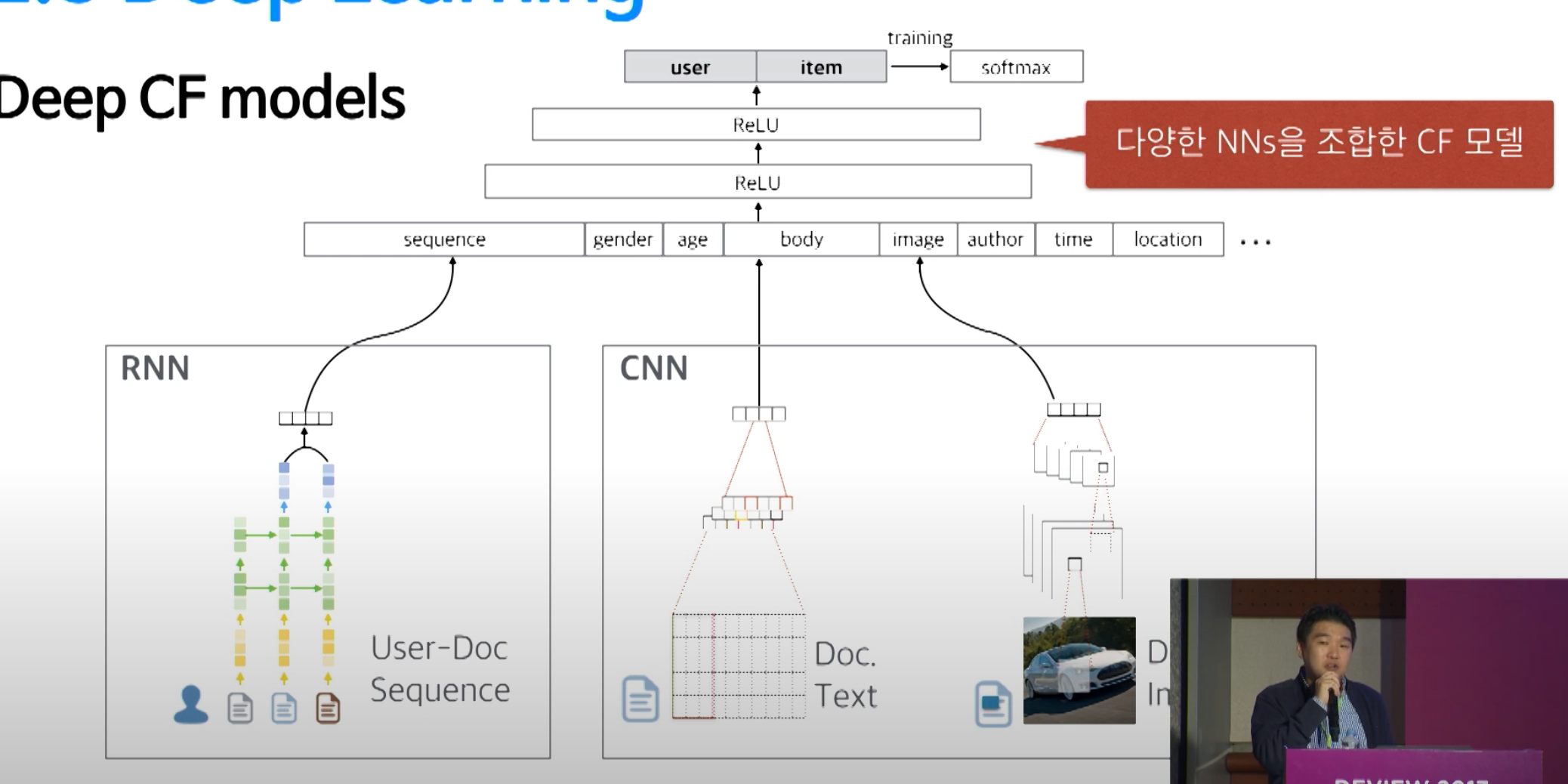
2-4) 추천 모델 특징 비교
- Statistics Based
- chi-squared : Categorical
- KL-Divergence : Continuous
→ 통계&확률
- Collaborative Filtering
- Neighborhood : Similarity(PMI)
- Matrix Factorization : Missing Data issue
→ 선형과 비선형
- Deep Learning
- RNN / CNN : Non-linearity
-
Deep CF : Neural Network
3. 추천 품질 평가 요소
1) 추천의 만족도
- Accuracy : 유저가 실제 소비한 아이템이 상위에 추천되는지 → 추천 모델의 성능
- Diversity : 다양한 주제/유형의 아이템이 잘 추천되는지
- Novelty : 새로 나온 최신의 아이템이 잘 추천되는지
2) 추천 모델 평가 방법
- 오프라인 정량평가
- low cost
- 전체 모델간 비교
- 유저 관심사 고정 → But 현실에서 실제 추천된 결과가 좋은 성능을 유지할 지 알 수 없음
- 온라인 A/B 테스트
- High Cost
- 특정 모델간 비교 평가 가능
- 유저 관심사 변화 → 실서비스 적용 여부 결정가능
3) 추천 모델 평가 방법
- 추천모델 정확도 평가 지표
-
- precision / Recall@N
- 추천의 경우 정해진 정답이 없는 경우도 많기에 하나의 정답값만을 확인하는 precision보다는 총 정답 문서중에, 모델이 얼만큼의 정답 문서를 찾아주는가를 확인하는 Recall을 주로 사용
-
- F-score / AUROC
- Recall이 임계치에따라 얼마나 robust하게 결과를 내는지 확인하기 위해 AUROC사용
-
- nDCG / MRR (normalized Discouted cumulative Gain / Mean Reciprocal Rank)
- 상위에 얼마나 정답값이 랭크가 되는지를 점수화하는 방법 → 모델 평가시 위의 방법론 활용
-
- 실서비스 만족도 평가지표
- 유저별 클릭수
- 유저별 총 체류시간
- 신규 아이템 회전율 → A/B Test 실행시 평가지표로 고민해 보면 좋을 듯
Reference
[1] https://www.youtube.com/watch?v=oTuM8WDI3nA