ACF & PACF
19 Mar 2021 ML: ARIMA또는 Prophet등 데이터의 과거 패턴만을 활용한 시계열 분석에 있어서 중요한 개념 중 하나가 자기상관함수(ACF : Aucto Correlation Function)와 편자기상관함수(PACF : Partial autocorrelation Fucntion)이다. 특히 Arima의 경우, 위 두가지 함수를 그려보며, 데이터의 자기상관성을 검토하여 파라미터(p,d,q)를 설정하니 각 개념에 대하여 살펴보자.
1. 자기상관함수(ACF : Aucto Correlation Function)
- ACF : $y_t$와 $y_{t+k}$사이의 Correlation을 측정하는 것
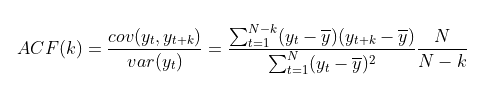
- 분자 : $var(y_t)$ : $N-K$관측값을 대상으로 계산하기에 K가 커지면 줄어듦.
- 분모 : $cov(y_t, y_{t+k})$ : 모든 N개의 관측치에 대해서 측정하기에 고정됨
∴ K가 커지면, 분자의 SUM값이 줄어들어 ACF(k)는 줄어든다. 다시말해 K가 커지면 오늘을 기점으로 먼 미래의 상관관계를 측정하는 것이기에, 자기상관계수는 줄어들게 된다.
+ 자기상관계수 vs 상관계수(PACF : Partial autocorrelation Fucntion)

2. 편자기상관함수(PACF : Partial autocorrelation Fucntion)
: 앞서 ACF만으로는 자기상관성(AR:Autocorrelation)모델과 이동평균(MA:MovingAverage)모델을 선택하거나, 얼만큼의 시차(lag)를 적용할지 결정하기 어렵다. 이에 추가로 PACF를 활용한 분석이 필요하다.
- PACF는 $y_t$와 $y_{t+k}$사이의 Correlation을 측정하는 것은 동일하나,
$t$와 $t_{+k}$사이의 다른 $y$값들의 영향력을 배제하고 측정한다. ‘ACF가’ ‘미분’이라면, ‘PACF’는 ‘편미분’과 유사해 보인다.
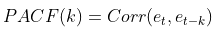
이때, $e_{t}$는 아래와 같으며,
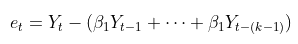 온전한 $y_{t}$와 $y_{t+k}$만을 남겨놓고, 둘 사이의 상관계수를 계산한다.
온전한 $y_{t}$와 $y_{t+k}$만을 남겨놓고, 둘 사이의 상관계수를 계산한다.
3. 차분(Differencing)
: ACF와 PACF는 시계열적인 특성만을 이야기한다. 때문에, 그래프 자체가 전체적으로 우상향/우하향 하는 선형적인 추세가 있다면, 시계열이 비정상(non-stationary)으로 작동하여 ACF와 PACF를 정확하게 살펴 볼 수 없다. 이러한 점을 해결하기위해, 데이터에 차분을 적용해 선형적인 추세를 없애 줄 수 있다. * 정상성 : 평균이 일정 -> 모든 시점에 대해서 일정한 평균을 갖음(평균이 일정하지 않은 시계열은 차분을 통해 정상화 가능)
- 1) 로그 변환을 통해 데이터의 스케일을 눌러줌
- 2) 이후 차분을 적용하여 선형적인 패턴 제거
- 3) ACF와 PACF를 진행하여 AR & MA 결정
df_time = pd.DataFrame(df_merge_fin[y_col])
# 2) 차분(1&2차) 확인
def time_series_diff(df_time_target, y_col) :
# 차분 -> 시계열 정상성 확인
df_time_target[y_col].plot(
figsize = (12,5),title = str(APP_KEY +' : orginal Non Stationary Data')).autoscale(axis = 'x', tight = True)
plt.show()
## 1차 차분
diff_1 = df_time_target[y_col]-df_time_target[y_col].shift(1) # 판다스의 shift메소드를 이용해 차분하는 방
plt.figure(figsize = (12,5))
plt.plot(diff_1)
plt.title(str(APP_KEY + ' : First Order of Non Stationary Data'))
plt.show()
## 2차 차분
diff_2 = np.diff(df_time_target[y_col], 2)
plt.figure(figsize = (12,5))
plt.plot(diff_2)
plt.title(str(APP_KEY + ' : Seconde Order of Non Stationary Data'))
plt.show()
time_series_diff(df_time, y_col)
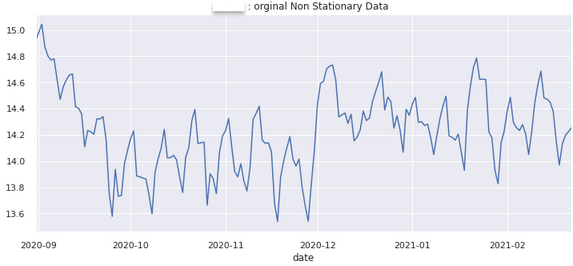
1차 차분
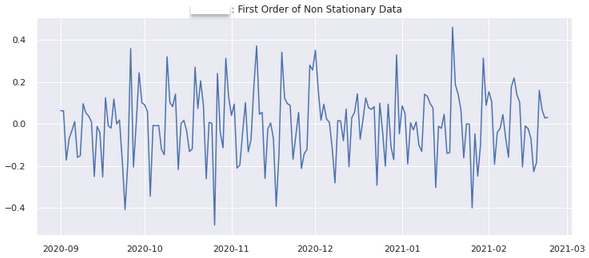
2차 차분
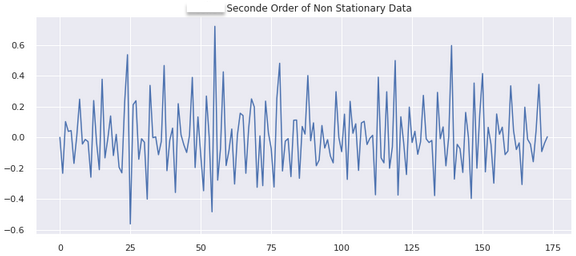
4. ACF와 PACF를 통한 모델(AR & MA) 및 시차 결정
-
- 1) ACF
- 자기 상관 함수는 k 시간 단위로 구분된 시계열의 관측치(yt 및 yt–k) 간 상관의 측도입니다.
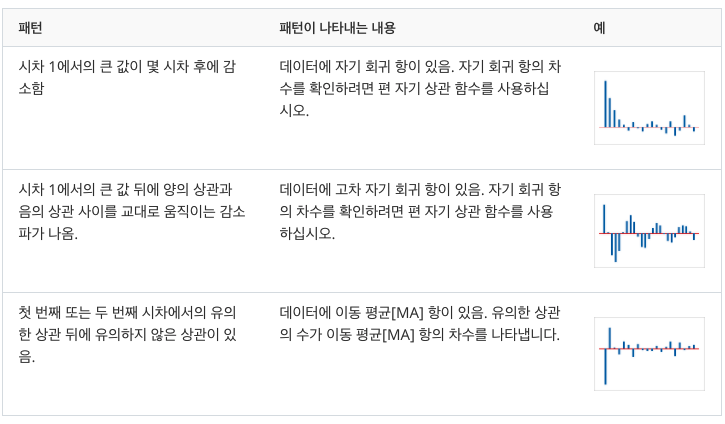
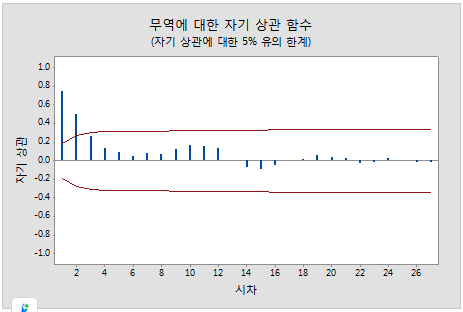 이 그림에서는 시차 1에 유의한 상관이 있고 몇 시차 후에 감소합니다.
이 패턴은 자기 회귀 항을 나타냅니다. 자기 회귀 항의 차수를 확인하려면 편 자기 상관 함수를 사용해야 합니다.
이 그림에서는 시차 1에 유의한 상관이 있고 몇 시차 후에 감소합니다.
이 패턴은 자기 회귀 항을 나타냅니다. 자기 회귀 항의 차수를 확인하려면 편 자기 상관 함수를 사용해야 합니다.
-
- 2) PACF
- 편 자기 상관 함수는 다른 모든 짧은 시차 항에 따라 조정한 후 k 시간 단위로 구분된 시계열(yt–1, yt–2, …, yt–k–1)의 관측치(yt 및 yt–k) 간 상관의 측도입니다.

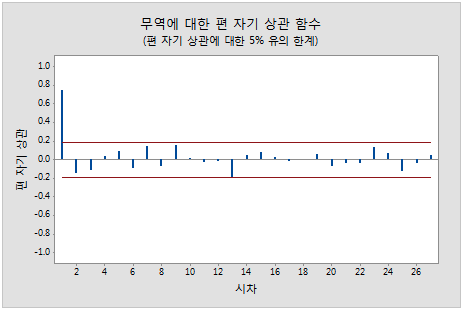 이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에 유의하지 않은 상관이 있습니다.
이 패턴은 1차 자기회귀 항을 나타냅니다.
이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에 유의하지 않은 상관이 있습니다.
이 패턴은 1차 자기회귀 항을 나타냅니다.
Reference
[1] 시계열(Time series) > ACF, PACF [2] [R] 자기상관계수 (Autocorrelation Coefficients), 자기상관그림(Autocorrelation Plot) [3] 자기 상관 그래프 (ACF Auto Correlation Function) [4] TimeSeries with Python - 차분 & 차분을 이용한 예측값 구하기