설문데이터 활용하기2 - 신뢰수준과 표본오차
25 Jan 2022 Statistics [KEY WORD]
#설문조사, #확률, #통계, #신뢰구간, #표본오차
설문 표본이 실제 모집단의 특성을 왜곡하지 않고 무작위 또는 층화 표집으로 추출되었더라도, 너무 적은 표본은 편향 및 오차를 포함할 수 있다. 따라서 통상 95% 신뢰수준하에서, 표본의 크기에 따른 표본 오차가 얼마나 발생하는지 측정하여야 설문 결과로 얻은 값이 우연의 일치인지, 아니면 통계적으로 유의미한 차이인지 확인할 수 있다.
1. 일반 관점, 신뢰수준과 표본오차
: 아래와 같은 여론조사가 있다고 할때, ‘신뢰수준’과 ‘표본오차’는 무엇일까.
1000명을 대상으로 조사한 결과, 38%는 A후보, 26%는 B후보, 24%는 C후보를 지지한다고 응답하였다. (95% 신뢰수준에 표본오차 ±3%)
1) 신뢰수준 95%
: 동일 조사 100번 수행시, 오차범위내 동일한 결과가 나올 횟수가 95번.
2) 표본오차 (신뢰수준 95%일 때)
: 동일 조사 100번 수행시, 95번은 오차가 ±3% 포인트 안에 있음.
- (1) 모집단 또는 표본의 표준편차를 알 때 : $\epsilon$ = $z \times \sqrt{\sigma^2\over n}$
- (2) 모집단 또는 표본의 표준편차를 모를 때 : $\epsilon$ = $z \times \sqrt{p(1-p)\over n}$
- (3) 모집단 또는 표본의 표준편차를 모르며, 모집단이 충분히 크지 않을 경우 : $\epsilon$ = $z \times \sqrt{p(1-p)(N-n)\over n((N-1))}$
- p : 특정 결과 발생 확률 (0.5가 가장 불확실성이 높기에, 표본 오차를 극대화 하기 위해선 0.5로 통상 설정)
- n : 표본 크기(Sample Size)
- N : 모집단(Population)
3) 해석
- A후보는 B,C 오차범위 밖에서 큰 차이로 앞선다.
→ 95% 신뢰수준으로, A가 B,C보다 높다고 할 수 있다. - B와 C 후보는 오차범위 내에 있다.
→ 95% 신뢰수준으로, B가 C보다 높다고 할 수 없다.
2. 통계 관점, 신뢰수준과 표본오차
- https://kuduz.tistory.com/1220 게시글 ‘오차범위(표본오차)란 무엇인가를 공부한 글입니다.’
1) 이항분포 (동전던지기)
(1) 2회 시행시, 앞면(H)이 N번 나올 확률 분포
- H, 0회 확률 : 1/4 [T,T]
- H, 1회 확률 : 2/4 [T,H], [H,T]
- H, 2회 확률 : 1/4 [H,H]
(2) 3회 시행시, 앞면(H)이 N번 나올 확률 분포
- H, 0회 확률 : 1/8 [T,T,T]
- H, 1회 확률 : 3/8 [T,T,H], [T,H,T], [H,T,T]
- H, 2회 확률 : 3/8 [T,H,H], [H,T,H], [H,H,T]
- H, 3회 확률 : 1/8 [H,H,H]
(3) 100회 시행시, 앞면(H)이 N번 나올 확률 분포
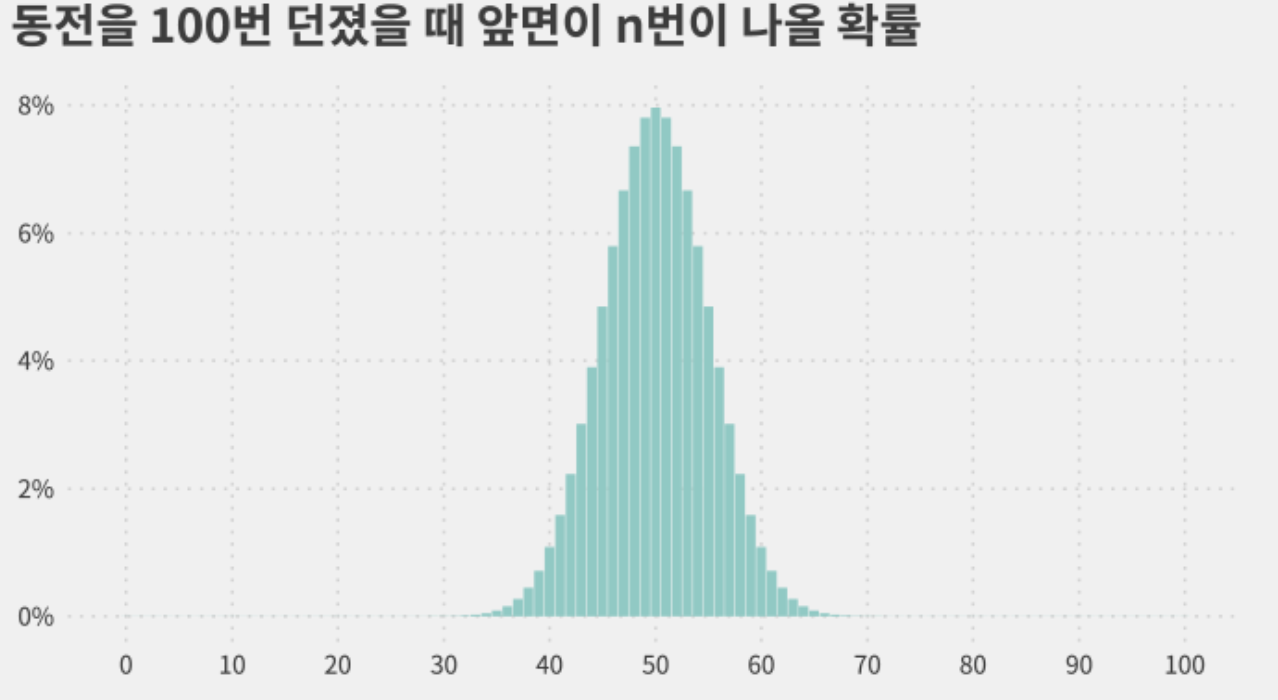
- 100번 던질 때, 앞면이 49~51회 나올 확률 : 23.6% (7.8% + 8% + 7.8%)
- 100번 던질 때, 앞면이 40~60회 나올 확률 : 95.4% 무려 95%의 확률이 가운데 20회의 경우에 발생한다…!?!? 정규분포의 형태를 띄어감!
2) 정규분포
: 앞서 동전던지기를 통해, 이항분포가 정규분포를 띄고 있음을 보았다. 따라서 정규분포의 특징을 정리하면 아래와 같다.
- 평균이 가장 볼록하고, 평균에서 멀어질 수록 높이가 낮아지는 분포
- 평균($\mu$) & 표준편차($\sigma$)에 따라 모양이 변함
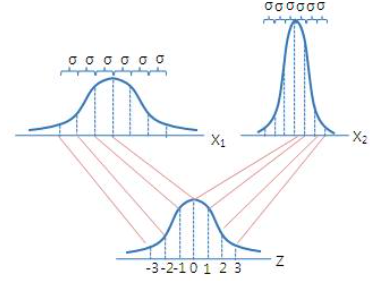
3) “표준”정규분포
: 위 정규분포는 평균과 표준편차에 따라서, 모두 모양이 제각각이다보니, 특정 확률(ex.95%)를 규정하려면 정규분포마다 서로 다른 표준편차값이 설정될 것이다. → 때문에 정규분포에서 평균을 빼고, 표준편차로 나눠 ($Z$ = $(X - \mu)\over\sigma$) 평균이 0이고, 표준편차가 1인 ‘표준’정규분포로 변환하여 규격화해보자.
- 평균($\mu$) : 0
- 표준편차($\sigma$) : 1
4) 신뢰구간(confidence_interval)
: 이렇게 ‘표준정규분포’를 얻었고, 우리는 대략 2표준편차, 정확히는 $\pm$1.96$\sigma$ 안에 전체 사례의 95%가 포함됨을 앞서 동전사례를 통해 알고 있습니다. 따라서 95% 신뢰구간이라하면 +1.96$\sigma$ ~ +1.96$\sigma$로 표현 하며, 오차범위 & 표본오차라고도 부릅니다.
5) 신뢰수준(confidence_level)
: 그렇다면 ‘신뢰수준’의 의미는 무엇일까.
- 평균이 0, 표준편차가 1인 (표준)정규분포를 따르는 모집단이 있을 때,
- 샘플(표본) 50개를 뽑고, 이 샘플의 평균과 표준편차를 계산하면,
- 각 샘플의 신뢰구간 100개 가운데, 95개(95%)는 샘플의 신뢰구간안에 모집단의 평균(0)이 위치할 것이라는 것.(물론 정확히 95%는 아니겠지만 95%에 수렴)
- 즉, 신뢰수준 95%는 100번 조사했을 때, 95번은 모집단의 값을 예측할 수 있지만, 5번 정도는 틀릴 수 있다는 뜻이 됩니다.
6) 샘플(표본)로 모집단 유추하기
: 앞서 신뢰수준을 이야기할 때, 우리는 모집단의 평균(모평균)이 0이라고 가정했기에, 표본 95개의 신뢰구간안에 모평균이 위치함을 알 수 있었습니다. 그러나 현실 및 여론조사에서 모집단의 평균을 알 수 없습니다. 이럴 때는 어떻게 신뢰수준 95%를 확인 할 수 있을까요. 샘플을 활용하여, 모집단의 평균을 추정할 수 있는지 확인해 봅시다.
(a) 모집단
- 모집단 : [1,2,3]
- 모평균($\mu$) : 2
- 모분산($\sigma^2$) : $2\over3$ = ( $(1-2)^2 + (2-2)^2 + (3-2)^2)\over3$ )
- 모표준편차($\sigma$) : $\sqrt{2\over3}$
(b) 표본
: 2개의 샘플을 추출(반복추출 허용)할 때 모든 경우의 수는 아래 테이블과 같음.
| 표집 | 표본 평균 | 오차(표본평균 - 모평균) | 오차 제곱 |
|---|---|---|---|
| [1,1] | 1 | 1 | 1 |
| [1,2] | 1.5 | 0.5 | 0.25 |
| [1,3] | 2 | 0 | 0 |
| [2,1] | 1.5 | 0.5 | 0.25 |
| [2,2] | 2 | 0 | 0 |
| [2,3] | 2.5 | -0.5 | 0.25 |
| [3,1] | 2 | 0 | 0 |
| [3,2] | 2.5 | -0.5 | 0.25 |
| [3,3] | 3 | -1 | 1 |
| 평균 | 2 | 0 | $1\over3$ |
- 표본 평균의 평균($\bar{X}$) : 2
- 표본 분산($S^2$) : $1\over3$
- 표본 표준편차 -> 표준오차($S$) : $\sqrt{1\over3}$
(c) 표본평균과 모집단의 관계
: 우리는 표본평균으로부터 위와 같은 통계치들을 얻을 때, 아래와 같은 사실을 확인 할 수 있습니다.
- 표본평균의 평균은 모평균과 같다. → [$\bar{x} = \mu$]
- 표본평균의 오차 제곱의 평균 즉 분산은, 모분산을 표본의 크기로 나눈값과 같다. → [$S^2$ = $\sigma^2\over n$]
- 표본평균의 표준편차(= 표준오차) → [$S$ = $\sqrt{\sigma^2\over n}$]
모집단의 평균과 분산도 알 수 있다는 이야기!"
(d) 모분산을 모른다면?
특정 관측치가 나타날 확률을 p라고 할 때, 기댓값($E(X)$) = 관측값 x 발생확률 = “n X p”라고 표현 할 수 있습니다.
그렇다면 다시 동전으로 돌아가 앞면에 1, 뒷면을 0에 값으로 부여 할때, 각면의 발생 확률(p) = $1\over2$입니다.
1) 따라서 기댓값은 아래와 같이 쓸 수 있고,
2) 분산은 편차의 제곱에 평균이기에, 편차의 제곱값에 각 편차의 발생확률을 곱해준것과 같습니다.
3) 위 식을 일반화 시키면 아래와 같습니다.
4) 앞서 표본의 표준편차(표준오차)($S$)은 아래 공식과 같았습니다.
5) 위 표준오차의 분산($\sigma^2$)자리에, 위에서 찾은 발생확률 p로 계산한 분산을 대입하면 아래와 같습니다.
6) 자 이제, 모집단의 분산을 모르더라도 표준오차를 계산할 수 있게되었습니다.
1표준오차가 위 공식과 같을 때, 우리는 앞서 95% 신뢰수준하에서 표준오차의 범위(오차범위[$\epsilon$])를 알고 싶습니다.
양측으로 2표준편차(정확히 1.96표준편차)에서 95%의 값을 포함하고 있기에, 표준오차 공식에 1.96이라는 z-score를 곱해줍니다.
(2표준편차라고 이야기할 때 ‘2’가 z-score이며, 95%는 1.96이됩니다.)
7) 표준오차를 활용하여, 실제 통계치 비교하기
: 이제 설문조사 결과를, 표준오차를 활용한 신뢰구간의 범위로 확장하여 다시 살펴보겠습니다.
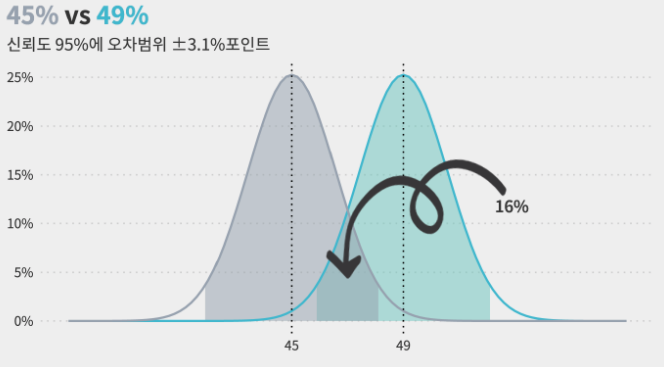
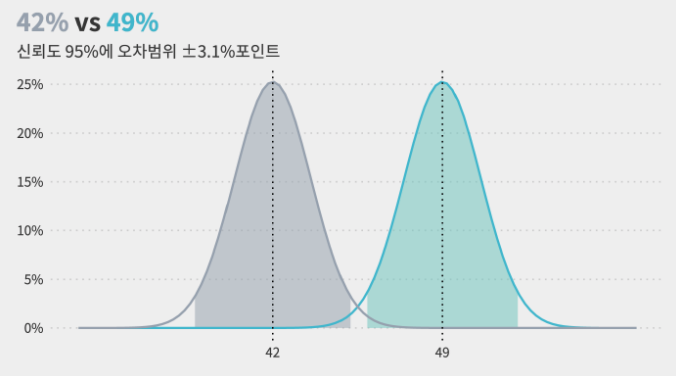
- 표본 오차 3.1%포인트일때, 긍정평가 49%의 신뢰구간 = 45.9% ~ 52.1%
- 표본 오차 3.1%포인트일때, 부정평가 45%의 신뢰구간 = 41.9% ~ 48.1% $\therefore$ 두 응답의 오차범위가 서로 중첩되기에, 긍정평가가 더 높다는 설문결과는 95%신뢰수준을 만족하지 못하고 결과가 뒤집힐 수 있습니다.
- 표본 오차 3.1%포인트일때, 긍정평가 49%의 신뢰구간 = 45.9% ~ 52.1%
- 표본 오차 3.1%포인트일때, 부정평가 41%의 신뢰구간 = 37.9% ~ 44.1% $\therefore$ 두 응답의 오차범위가 서로 벗어나 있기에, 긍정평가가 더 높다는 설문결과는 신뢰도 95% 기준으로 차이가 있다고 할 수 있습니다.
해설이 아니라 소설이다."
Reference
[1] 오차범위(표본오차)란 무엇인가?
[2] 표준오차, 표본오차, 오차한계 개념 구분
[3] Standard Normal Distribution, Standard Gaussian Distribution