10 May 2021
1. why use generator?
(1) Memory issue
: for-loop는 , 돌아야하는 list전체를 메모리에 올려놓은 상태로 작업을 시작하게된다. 때문에 list의 크기가 큰 경우, 차지하는 메모리가 커진다.
반면, generator는 값을 한꺼번에 메모리에 적재 하지 않고, next() 메소드를 통해 차례로 값에 접근할 때마다 메모리에 적재한다.
import sys
sys.getsizeof( [i for i in xrange(100) if i % 2] ) # list
# 536
sys.getsizeof( [i for i in xrange(1000) if i % 2] )
# 4280
sys.getsizeof( (i for i in xrange(100) if i % 2) ) # generator
# 80
sys.getsizeof( (i for i in xrange(1000) if i % 2) )
# 80
(2) Lazy evaluation : 계산 결과 값이 필요할 때까지 계산을 늦추는 효과
: 아래 예제를 보면, 일반 list는 list 내부 함수를 먼저 실행하여 값들을 모두 대기시켜놓은 후 for문을 통해 하나씩 추출한다. 때문에 리스트 내부의 함수 연산이 오래걸린다면, for문 자체의 실행이 늦춰진다.
# list 생성
list = [sleep_func(x) for x in xrange(3)]
for i in list:
print i
# <결과>
# sleep... # (1) list : 내부 [sleep_func(x) for x in xrange(5)] 함수 먼저 실행
# sleep...
# sleep...
# 0 # (2) list : 이후 for loop 실행
# 1
# 2
반면, generator는 for문이 수행 될 때마다 추출해야하는 값의 연산을 그때 그때 진행하기에 수행 시간이 긴 연산을 필요한 시점까지 늦출 수 있다는 특징이 있다.
# generator 생성
gen = (sleep_func(x) for x in xrange(3))
for i in gen:
print i
# <결과>
# sleep... # (1-1) generator 추출할 첫번째 값의 함수 실행
# 0 # (1-2) 이후 for loop 진행
# sleep... # (2-1) generator 추출할 두번째 값의 함수 실행
# 1 # (2-2) 이후 for loop 진행
# sleep...
# 2
2. How to use generator?
(1) 함수로 생성
: generator를 생성하는 방법은 2가지가 있다.
첫번째는 for loop를 통해 값을 하나씩 반환하는 일반 함수를 생성하되, 반횐하는 함수를 return 대신 yield 를 사용하는 방법이다.
# data
df = pd.DataFrame(
key_id : ['a','b','c'],
value : [1,2,3]
)
# make generator
def gen(df_tmp) :
for idx in df_tmp['key_id'] :
yield idx
idx_gen = gen(df_tmp)
# use generator by 'next'
while True :
try :
next(idx_gen)
except StopIteration :
break
(2) Generator expression
두번째는 generator expression를 사용하는 방법이다.
# make generator by generator expression
idx_gen = ( i for i in df_tmp.index )
# use generator by 'next'
next(idx_gen)
3. What is generator?
시간이 좀 있다면, generator가 어떻게 작동하는지도 자세히 살펴보자.
generator는 iterator 를 생성해 주는 function으로 next() 메소드를 사용해, 데이터에 순차적으로 접근가능한 ‘object’다. generator자체를 만드는데 있어서는 return 대신 yield라는 구문을 사용한다는 점을 제외하면 일반 함수와 큰 차이점이 없다.
그렇다면, yield와 일반 함수의 return의 차이점을 살펴보자
return : 함수 사용이 종료되면, 결과값을 호출하여 반환(return)후 함수 자체를 종료한다.(즉, 함수가 완전히 모두 실행 후 종료)yield :
(1) 특정함수(주로 generator함수)가 yield를 만나게 되면,
(2) 그 기점에서 함수를 잠시 정지 후 반환값을 next()를 호출한 쪽으로 전달한다.
(3) 이후 함수는 종료되지 않고, 유지된 상태로 남아있게 된다.
아래 예시를 살펴보자.
def generator(n) :
i = 0
while i < n :
yield i
i += 1
for x in generator(5) :
print(x)
# <결과>
# 0
# 1
# 2
# 3
# 4
# (1) for 문이 실행되며, 먼저 generator 함수가 호출된다.
# (2) generator 함수는 일반 함수와 동일한 절차로 실행된다.
# (3) 실행 중 while문 안에서 yield 를 만나게 된다. 그러면 return 과 비슷하게 함수를 호출했던 구문으로 반환하게 된다. 여기서는 첫번재 i 값인 0 을 반환하게 된다. 하지만 반환 하였다고 generator 함수가 종료되는 것이 아니라 그대로 유지한 상태이다.
# (4) x 값에는 yield 에서 전달 된 0 값이 저장된 후 print 된다. 그 후 for 문에 의해 다시 generator 함수가 호출된다.
# (5) 이때는 generator 함수가 처음부터 시작되는게 아니라 yield 이후 구문부터 시작되게 된다. 따라서 i += 1 구문이 실행되고 i 값은 1로 증가한다.
# (6) 아직 while 문 내부이기 때문에 yield 구문을 만나 i 값인 1이 전달 된다.
# (7) x 값은 1을 전달 받고 print 된다. (이후 반복)
4. Usage
1) list_sum
: generator와 dictionary 자료구조를 사용해 시간을 단축한 예제다.
무수히 많은 리스트가 존재하고, 해당 원소들의 개수를 모두 더해서 카운트해야하는 문제에서 많은 리스트를 제너레이트로 변환하고,
원소들을 dictionary형태의 key값으로 지정하여 개수를 카운트하였다.
def generate_list_sum(target_idx) :
"""
: [a,b,c] + [a,b,f] = {a : 2, b = 2, c = 1, f = 1}
"""
gen_list = (i for i in target_idx)
dict_counter = {}
while True :
try :
l = next(gen_list)
for k in l :
try :
dict_counter[k] += 1
except :
dict_counter[k] = 0
except StopIteration :
break
return dict_counter
Reference
[1] python generator(제너레이터) 란 무엇인가
19 Mar 2021
: ARIMA또는 Prophet등 데이터의 과거 패턴만을 활용한 시계열 분석에 있어서 중요한 개념 중 하나가 자기상관함수(ACF : Aucto Correlation Function)와 편자기상관함수(PACF : Partial autocorrelation Fucntion)이다. 특히 Arima의 경우, 위 두가지 함수를 그려보며, 데이터의 자기상관성을 검토하여 파라미터(p,d,q)를 설정하니 각 개념에 대하여 살펴보자.
1. 자기상관함수(ACF : Aucto Correlation Function)
- ACF : $y_t$와 $y_{t+k}$사이의 Correlation을 측정하는 것
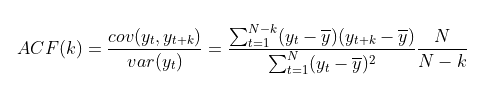
- 분자 : $var(y_t)$ : $N-K$관측값을 대상으로 계산하기에 K가 커지면 줄어듦.
- 분모 : $cov(y_t, y_{t+k})$ : 모든 N개의 관측치에 대해서 측정하기에 고정됨
∴ K가 커지면, 분자의 SUM값이 줄어들어 ACF(k)는 줄어든다. 다시말해 K가 커지면 오늘을 기점으로 먼 미래의 상관관계를 측정하는 것이기에, 자기상관계수는 줄어들게 된다.
+ 자기상관계수 vs 상관계수(PACF : Partial autocorrelation Fucntion)

2. 편자기상관함수(PACF : Partial autocorrelation Fucntion)
: 앞서 ACF만으로는 자기상관성(AR:Autocorrelation)모델과 이동평균(MA:MovingAverage)모델을 선택하거나, 얼만큼의 시차(lag)를 적용할지 결정하기 어렵다. 이에 추가로 PACF를 활용한 분석이 필요하다.
- PACF는 $y_t$와 $y_{t+k}$사이의 Correlation을 측정하는 것은 동일하나,
$t$와 $t_{+k}$사이의 다른 $y$값들의 영향력을 배제하고 측정한다.
‘ACF가’ ‘미분’이라면, ‘PACF’는 ‘편미분’과 유사해 보인다.
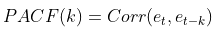
이때, $e_{t}$는 아래와 같으며,
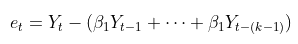 온전한 $y_{t}$와 $y_{t+k}$만을 남겨놓고, 둘 사이의 상관계수를 계산한다.
온전한 $y_{t}$와 $y_{t+k}$만을 남겨놓고, 둘 사이의 상관계수를 계산한다.
3. 차분(Differencing)
: ACF와 PACF는 시계열적인 특성만을 이야기한다. 때문에, 그래프 자체가 전체적으로 우상향/우하향 하는 선형적인 추세가 있다면, 시계열이 비정상(non-stationary)으로 작동하여 ACF와 PACF를 정확하게 살펴 볼 수 없다.
이러한 점을 해결하기위해, 데이터에 차분을 적용해 선형적인 추세를 없애 줄 수 있다.
* 정상성 : 평균이 일정 -> 모든 시점에 대해서 일정한 평균을 갖음(평균이 일정하지 않은 시계열은 차분을 통해 정상화 가능)
- 1) 로그 변환을 통해 데이터의 스케일을 눌러줌
- 2) 이후 차분을 적용하여 선형적인 패턴 제거
- 3) ACF와 PACF를 진행하여 AR & MA 결정
df_time = pd.DataFrame(df_merge_fin[y_col])
# 2) 차분(1&2차) 확인
def time_series_diff(df_time_target, y_col) :
# 차분 -> 시계열 정상성 확인
df_time_target[y_col].plot(
figsize = (12,5),title = str(APP_KEY +' : orginal Non Stationary Data')).autoscale(axis = 'x', tight = True)
plt.show()
## 1차 차분
diff_1 = df_time_target[y_col]-df_time_target[y_col].shift(1) # 판다스의 shift메소드를 이용해 차분하는 방
plt.figure(figsize = (12,5))
plt.plot(diff_1)
plt.title(str(APP_KEY + ' : First Order of Non Stationary Data'))
plt.show()
## 2차 차분
diff_2 = np.diff(df_time_target[y_col], 2)
plt.figure(figsize = (12,5))
plt.plot(diff_2)
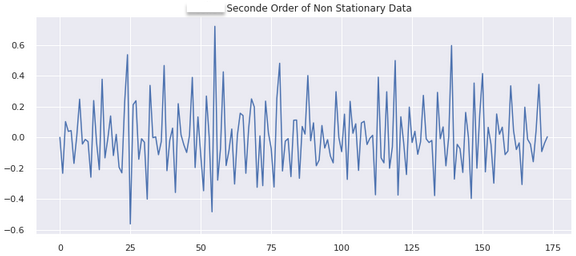
plt.title(str(APP_KEY + ' : Seconde Order of Non Stationary Data'))
plt.show()
time_series_diff(df_time, y_col)
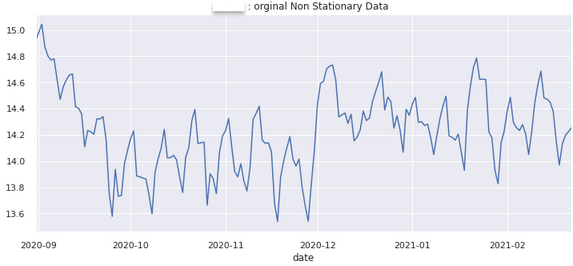
1차 차분
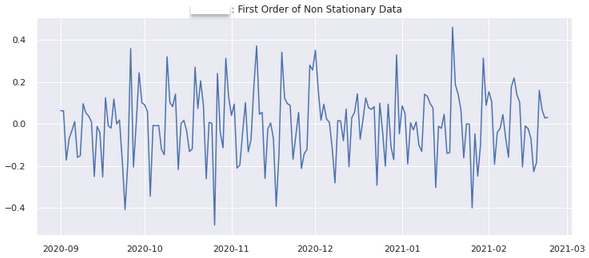
2차 차분
4. ACF와 PACF를 통한 모델(AR & MA) 및 시차 결정
-
- 1) ACF
- 자기 상관 함수는 k 시간 단위로 구분된 시계열의 관측치(yt 및 yt–k) 간 상관의 측도입니다.
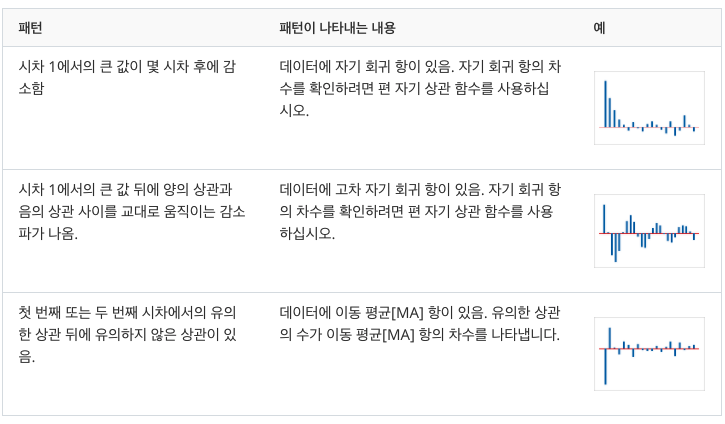
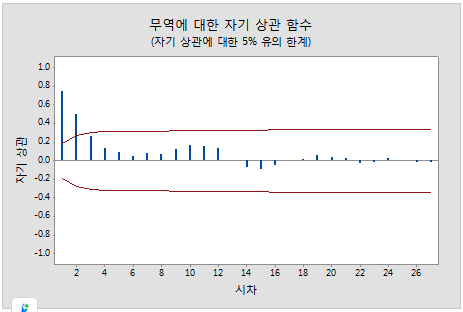 이 그림에서는 시차 1에 유의한 상관이 있고 몇 시차 후에 감소합니다.
이 패턴은 자기 회귀 항을 나타냅니다. 자기 회귀 항의 차수를 확인하려면 편 자기 상관 함수를 사용해야 합니다.
이 그림에서는 시차 1에 유의한 상관이 있고 몇 시차 후에 감소합니다.
이 패턴은 자기 회귀 항을 나타냅니다. 자기 회귀 항의 차수를 확인하려면 편 자기 상관 함수를 사용해야 합니다.
-
- 2) PACF
- 편 자기 상관 함수는 다른 모든 짧은 시차 항에 따라 조정한 후 k 시간 단위로 구분된 시계열(yt–1, yt–2, …, yt–k–1)의 관측치(yt 및 yt–k) 간 상관의 측도입니다.

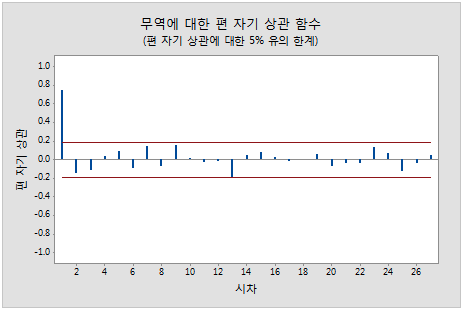 이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에 유의하지 않은 상관이 있습니다.
이 패턴은 1차 자기회귀 항을 나타냅니다.
이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에 유의하지 않은 상관이 있습니다.
이 패턴은 1차 자기회귀 항을 나타냅니다.
Reference
[1] 시계열(Time series) > ACF, PACF
[2] [R] 자기상관계수 (Autocorrelation Coefficients), 자기상관그림(Autocorrelation Plot)
[3] 자기 상관 그래프 (ACF Auto Correlation Function)
[4] TimeSeries with Python - 차분 & 차분을 이용한 예측값 구하기
18 Mar 2021
: 무심코 Nan과 None을 동일한 존재로 생각하고 있었다.
그러다, 분명 모든 결측치를 제거하였는데, 아래와 같은 에러가 뜨는 것을 확인하였다.
Value too large for dtype('float64') sklearn.preprocessing .StandardScaler()
문제의 원인은 무한대 값이 포함되어 있는 것이었으나, 이 과정에서 무한대가 Nan으로도 표현될 수 있다는 글을 보고 두 표기의 차이점을 확인해보고자 한다.
1. None
None = NULL
: 타 프로그램의 Null값으로, 즉 아무것도 없는 데이터를 의미한다.
# None 확인 방법
a = None
import pandas as pd
pd.isnull(a)
2. NaN
NaN = Not A Number
: 반면 NaN은 표현되지 않은 부동소수점 값으로, Python에서는 float타입이 됨.
# nan 확인 방법
b = float('Nan')
import math
math.isnan(b)
Reference
[1] (python)None, NaN에 대해서
[2] Value too large for dtype(‘float64’) sklearn.preprocessing .StandardScaler()
07 Mar 2021
1. Misunderstanding
1) GA는 분석 도구가 아닌, 측정 도구다.
- 측정 : 웹사이트의 다양한 구성요와 활동을 측정
- 분석 : 반면, 분석은 측정된 결과를 이용하여, 다양한 웹사이트의 결과와 원인을 분석
단순 몇가지 양적인 지표(이탈율, 체류시간 등등)만으로 현황을 평가하는 건 위험 할 수 있다.
GA가 보여주는 고객의 행동 데이터(양적 데이터)와 고객의 질적 데이터를 결합하여 분석해야 한다.
2) 데이터만 보면서 인사이트를 발굴한다는 착각
: 문제의식 및 문제정의를 명확히 하고, 데이터로 확인하는 과정을 거쳐야지, 데이터만 무작정 처다보며 결과를 도출하려는 사고방식에서 벗어나자.
- 마케팅 목표를 달성 하기 위해, 아이디어를 도출하는 것
- 가설을 수립하기 위해, 분석을 하는 것 이고
- 분석을 하기 위해 데이터를 확인하는 것이고,
- 데이터를 확인하기 위해, 측정을 하는 것
Reference
[1] ㅍㅍㅅㅅ-디지털 데이터 분석툴 구글 애널리틱스 클래스
08 Feb 2021
AIC & BIC는 CV(cross validation)처럼 모델의 적합도를 판단하여 파라미터에 따른 모델을 선택하기 위해서 사용되는 확률적 모델 선택 방법론(‘Probabilistic Model Selection’ or ‘information criteria’)이다.
두 방법의 장점으로는 K-fold CV처럼, 샘플 데이터를 설정하는 hold-out test set이 필요 없다는 장점이 있으나, 불확실성을 충분히 고려하지 않아 모델 선택 과정이 단순화 될 수 있다는 한계점 또한 존재한다.
0. Probabilistic Model Selection
-
- Model Performance
- How well a candidate model has performed on the training dataset.
-
- Model Complexity
- How complicated the trained candidate model is after training.
1. AIC
AIC = -2/N * LL + 2 * k/N
2. BIC
BIC = -2 * LL + log(N) * k
Reference
[1] Probabilistic Model Selection with AIC, BIC, and MDL
[2] AIC(Akaike information criterion)
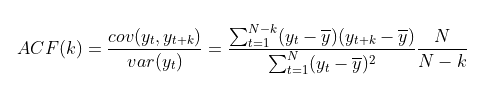

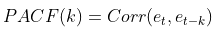
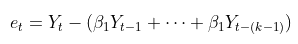 온전한 $y_{t}$와 $y_{t+k}$만을 남겨놓고, 둘 사이의 상관계수를 계산한다.
온전한 $y_{t}$와 $y_{t+k}$만을 남겨놓고, 둘 사이의 상관계수를 계산한다.




 이 그림에서는 시차 1에 유의한 상관이 있고 몇 시차 후에 감소합니다.
이 패턴은 자기 회귀 항을 나타냅니다. 자기 회귀 항의 차수를 확인하려면 편 자기 상관 함수를 사용해야 합니다.
이 그림에서는 시차 1에 유의한 상관이 있고 몇 시차 후에 감소합니다.
이 패턴은 자기 회귀 항을 나타냅니다. 자기 회귀 항의 차수를 확인하려면 편 자기 상관 함수를 사용해야 합니다.

 이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에 유의하지 않은 상관이 있습니다.
이 패턴은 1차 자기회귀 항을 나타냅니다.
이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에 유의하지 않은 상관이 있습니다.
이 패턴은 1차 자기회귀 항을 나타냅니다.