19 Jan 2021
: 여러개의 변수를 loop문을 활용하여 자동으로 생성하는 방법.
1. Dynamically create variable
1) globals() 함수
: globals()함수를 사용하여, 동적으로 변수를 생성 할 수 있다.
nm_list = ['cat', 'dog', 'rat']
i = 0
for nm in nm_list :
globals()[nm] = [x for x in range(i)]
# cat = [0]
# dog = [0,1]
# rat = [0,1,2]
: 할당 과정에서 format() 함수를 사용해, 규칙성을 있는 변수 목록 생성하기
nm_list = ['cat', 'dog', 'rat']
i = 0
for nm in nm_list :
i += 1
globals()['animal_{}'.format(nm)] = [x for x in range(i)]
# animal_cat = [0]
# animal_dog = [0,1]
# animal_rat = [0,1,2]
Reference
[1] 변수 이름을 loop 돌려서 할당하기
28 Dec 2020
[KEY WORD]
#상관관계, #PearsonCorrelation,
#관계강도, #Spearman,
#자기상관, #autocorrelation,
#인과관계, #GrangerCausality
Pearson 상관관계
1) 변수 사이의 ‘선형’ 관계 조사(pearson)
: 두 계량형 변수 사이의 선형 관계의 강도와 방향을 확인
Spearman & Kendall 단조 상관관계
1) 선형관계와 단조관계 차이
: 앞선 pearson의 상관관계는 선형관계만을 표현 할 수 있을 뿐, 두 변수간의 관계가 곡선일 경우 Pearson의 상관관계는 이를 표현하지 못하게 되므로 관계성만을 표현해주는 Spearman 또는 Kendall의 단조관계 필요.
2) Spearman & Kendall
- 변수값 대신 순위로 바꿔서 용하는 상관계수(학교 등급, 졸업 학위)
- 비모수 검정
- Spearman : 데이터 내 편차와 애러에 민감하며, 일반적으로 켄달의 상관계수보다 높은 값을 가짐.
- Kendall : 샘플 사이즈가 적거나, 데이터의 동률이 많을 때 유용
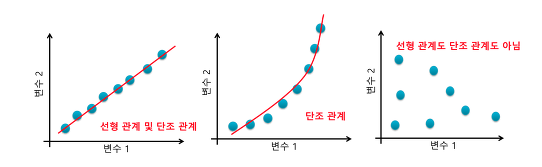 선형관계라면 단조관계이지만,
단조관계라고 선형관계는 아니다.
선형관계라면 단조관계이지만,
단조관계라고 선형관계는 아니다.
자기상관(autocorrelation) + 자기 회귀
1) 자기상관(autocorrelation)
: 시간 또는 공간적으로 연속된 일련의 관측치들간에 존재하는 상관관계로, 현재의 상태가 과거와 미래의 상태에 밀접한 연관을 지니는 경우.
2) 자기회귀(autoregression)
: 회귀분석에서 시계열의 관측값이 선행된 관측값에 의존하여 상관관계를 보일 때, 즉 관측값이 선행관측값들의 회귀관계를 갖는 현상을 자기회귀 (autoregression)이라 한다.
자기 회귀 현상이 발생하면, OLS방식에 의하여 추정된 회귀계수가 비록 불편성(편향이 발생하지 않은)을 만족할지라도 최적합치일 수 없다. 또한 자기회귀가 발생하는 경우, 일반적으로 t값과 f값 및 $R^2$값이 실제보다 증가하는 경향이 있음.
자기상관(autocorrelation)
인과 관계
: A와 B사이의 ‘원인’ - ‘결과’ 분석을 하고 싶다면, ‘회귀분석’ 또는 ‘GrangerCausality’ 분석 진행
Reference
[1] 자기상관(autocorrelation)
[2] 상관관계 분석(correlation analysis)
[3] 공분산과 상관관계(covariance_correlation)
[4] 인과관계_elearning(GrangerCausality)
30 Nov 2020
: 데이터 전처리 단계에서 변수별 스케일이 서로 다르기에 이를 조정하기 위한 sclaling과정을 자주 거치게 된다. 위 3가지 방법은 데이터를 학습이 용이한 형태로 변형한다는 유사점을 갖고 있지만, 각 방법마다 상황에 맞게 사용하기 위해서 차이점을 구분해보자.
1. Rescale
1) Normalization
(1) min-max Normalization[0~1]
- - 목표 : 데이터의 상대적 크기에 대한 영향력을 줄이기
- Normalization은 변수의 스케일(scaling)을 [0,1]로 재조정한다.
- 특히 변수 1개 보다, 여러개의 변수가 서로 비교되어야 할 때, 특정 변수의 단위가 너무 커 상대적 영향력이 과대 평가되는 것을 방지하기 위해 사용됨.
- 단, 각 변수내에 이상치가 없다는 가정하에 사용하는 것이 적절하다.
$x' = \dfrac{x - min(x)}{max(x) - min(x)}$
from sklearn.preprocessing import MinMaxScaler
scaler = MInMaxScaler()
df[:] = scaler.fit_transform(df[:])
df[:] = scaler.fit_transform(df['col_1']) # 하나의 열에 한하여 Normalization을 진행하고 싶은 경우,
(2) Mean Normalization[-1~1]
- - 목표 : 데이터가 평균보다 큰지 작은지 표현(이상치에 영향을 받을 가능성 존재)
- 영화 선호 평가(rating)처럼 데이터의 값이 {1,2,3,4,5}와 같은 경우, 평균값을 기점으로 평균이하에는 음의 수치를, 이상에는 양의 수치를 주고 적용하고 싶은 경우 Mean Normalization이 더 적절하다.
$x' = \dfrac{x - mean(x)}{max(x) - min(x)}$
2) Standardization(표준화)
- - 목표 : 데이터가 평균으로부터 떨어진 정도를 표현
- Standardization(표준화)는 ‘전처리’ 단계에서 변수의 평균을 0으로 조정하고 개별 단위 분산으로 값을 재조정(scaling)하기 위해 자주 사용된다.
표준화를 거쳐 +/-1.96(또는2)를 넘는 데이터 제거할 수 있음.
$x' = \dfrac{x - \mu}{\sigma}$
from scipy import stats
df['col_std'] = stats.zscore(df['col_raw'])
df = df[df['col_std'].between(-2,2)] # outlier detection
+ 위 방법들은 독립적이지 않고, 아래와 같이 두 방법을 모두 거쳐 사용하기도 한다.
- (1) Standardization(표준화)으로 outlier 제거하기
- (2) Normalization(정규화)으로 scale의 상대적 크기 영향력을 줄여 분석에 투입
2. Regularization
: 위에서 언급한 Normalization & Standardization은 스케일링의 개념만을 갖고 있다면,
Regularization은 ‘Overfitting’의 문제를 해결하기 위해 등장한다. 모델에 추가적인 loss Function(손실 함수)을 추가함으로써, 모델의 파라미터가 더 작은 값으로 수렴하게 되어(중요하지 않은 변수의 영향력 축소) 과적합을 현저하게 낮추는 효과를 갖는다.
import numpy as np
from sklearn import preprocessing
X = np.asarray([
[-1,0,1],
[0,1,2]],
dtype=np.float) # Float is needed.
# Before-normalization.
print(X)
# Output,
# [[-1. 0. 1.]
# [ 0. 1. 2.]]
1) L1-Norm : Lasso
- 목표 : 절대값 함수는 0에서 미분이 불가하기에, Sparse한 모델을 트레이닝할때, 불필요한 변수의 파라미터를 완전히 0으로 만들 수 있어 차원을 줄이는데 유용합니다.
${\lVert x \rVert}_p = \sqrt[p]{\sum_{i = 1}^{n} {\lvert x_i \rvert}^p}$
X_normalized_l1 = preprocessing.normalize(X, norm='l1')
print(X_normalized_l1)
# [[-0.5 0. 0.5]
# [ 0. 0.3 0.67]]
# Absolute value of all elements/features.
X_abs = np.abs(X_normalized_l1)
print(X_abs)
# [[0.5 0. 0.5]
# [0 0.3 0.67]]
# Sum over the rows.
X_sum_abs = np.sum(X_abs, axis=1)
print(X_sum_abs)
# Output,
# [ 1. 1.]
# Yay! Each row sums to 1 after being normalized.
- 목표 : 반면 L2는 변수의 파라미터를 완전히 0으로 만들지 않기에,
주어진 조건이 명확하지 않거나 부족한 ill-posed problem에서 더 자주 선호됩니다.
: $F(x) = f(x) + \lambda {\lVert x \rVert}_2^2$
# l2-normalize the samples (rows).
X_normalized = preprocessing.normalize(X, norm='l2')
# After normalization.
print(X_normalized)
# Output,
# [[-0.70710678 0. 0.70710678]
# [ 0. 0.4472136 0.89442719]]
# Square all the elements/features.
X_squared = X_normalized ** 2
print(X_squared)
# Output,
# [[ 0.5 0. 0.5]
# [ 0. 0.2 0.8]]
# Sum over the rows.
X_sum_squared = np.sum(X_squared, axis=1)
print(X_sum_squared)
# Output,
# [ 1. 1.]
# Yay! Each row sums to 1 after being normalized.
Reference
[1] Differences between Normalization, Standardization and Regularization
[2] 데이터 표준화(Standardization), 정규화(Normalization) 차이점
30 Oct 2020
Q Adding values in two lists
: 두개의 리스트 내부에 있는 값들을 더하는 너무 간단한 문제이다.
그러나 생각보다 코드가 길어져서 골머리를 앓다가, zip을 사용하니 허무하게도 쉽게 문제가 해결되었다.
zip
: zip은 동일한 개수로 이루어진 자료형을 묶어 주는 역할을 한다.
list_A = [1,2,3,4]
list_B = ['a', 'b', 'c', 'd']
list(zip(Number,name))
# [(1,'a'),(2,'b'),(3,'c'),(4,'d')]
# make dict using zip
dic
for key, value in zip(list_A, list_B) :
dic[key] = value
print(dic)
# {1:'a', 2:'b', 3:'c', 4:'d'}
이렇게, 2개의 객체에서 순서대로 값을 하나씩 빼서 묶어주므로,
zip을 사용하면, 2개의 리스트의 각 원소별로 더할 수 있다!
Adding values in two lists using ‘zip’
zip을 사용한 리스트내 원소간 합 코드는 아래와 같다.
list_1 = [1,3,5,7]
list_2 = [10,20,30,40]
[x + y for x, y in zip(list_1, list_2)]
# [11, 23, 35, 47]
ETC
dict.items() : Get keys & Values from dictionary
: 키(Key) & 값(Value) 쌍을 리턴
dict_tmp = {"철수": 90, "민수": 85, "영희": 80}
# dict_items([('민수', 85), ('영희', 80), ('철수', 90)])
enumerate(list) : Get Index & Value from list
: 리스트내 인덱스(Index) & 값(Value) 쌍을 리턴.
lst_tmp = ['a', 'b', 'c']
for idx, value in enumerate(lst_tmp)
print(idx, value)
# 0,'a'
# 1,'b'
# 2,'c'
Reference
[1] Python zip 내장함수
[2] Add SUM of values of two LISTS into new LIST
25 Oct 2020
7. Azure Architecture Bigdata & ML
1) Azure BigData Services
(1) Azure SQL Data Warehouse
: 큰 규모의 데이터에서 복잡한 쿼리를 빠르게 실행할 수 있는 관리형 서비스
(2) Azure HDInsight
: Hadoop 파일 시스템을 사용하는 완전 관리형 분석 서비스. 방대한 양의 데이터를 보다 쉽고 빠르게 처리하며, 비용 효율적으로 처리 가능
(3) Azure Data Lake Analytics
: 빅데이터를 단순화하는 주문형 분산 작업 서비스. 데이터를 변환 및 추출에 사용
(4) Azure Databricks
: Apache Spark 환경을 사용하여 AI 솔루션을 빌드하며, 각종 ML 프레임워크와 라이브러리 제공
2) ML
(1) Azure Machine Learning Service
: 머신 러닝의 모델을 개발하고 교육, 테스트 배표, 관리, 추적을 하는데 사용되는 클라우드 기반 솔루션
(2) Azure Machine Learning Studio
: 사용자가 코드를 작성하지 않고, 머신러닝 솔루션을 구축하고 테스트 및 배포를 할 수 있는 솔루션. 드래그 앤 드롭 방식의 시각적 작업 영역을 제공
8. Serverless
- 클라우드 서비스 공급자가 서버를 실행하고 머신의 리소스를 동적으로 관리하는 클라우드 컴퓨팅 실행 모델
- 용량 단위 구매가 아닌, 소비 단위 구매
- 일반적으로 실행 횟수, 실행 시간(CPU), 실행 용량(memory)을 기반으로 과금
1) Serverless 서비스
(1) Azure Functions
: 기본 플랫폼이나 인프라를 구성하지 않고, 소스 코드를 실행할 수 있는 서비스. 이벤트 기반으로 동작
(2) Azure Logic App
: 앱, 데이터, 시스템, 서비스를 통합하여 작업 또는 비즈니스 프로세스 및 워크 플로를 자동화 할 수 있는 서비스
(3) Azure Event Grid
: 균일한 이벤트 소비를 위해 발행, 구독모델을 사용하는 완전 관리형 지능형 이벤트 라우팅 서비스
 선형관계라면 단조관계이지만,
단조관계라고 선형관계는 아니다.
선형관계라면 단조관계이지만,
단조관계라고 선형관계는 아니다.
